Bayes is Plural.
The strict application of probability rules (the Bayesian approach) forms the basis of artificial intelligence (AI) and empirical sciences (or data based sciences) because it ensures optimal beliefs given the available information. Probability rules have been known since the late 18th century and are conceptually intuitive: preserving the prior belief that remains consistent with the data (product rule) and predicting with the contribution of all hypotheses (sum rule). While nothing better has been proposed in practical terms during this time, its application has historically been limited due to the computational cost associated with evaluating the entire hypothesis space. At the turn of the 21st century, these obstacles have been partially overcome thanks to modern computational and algorithmic advances. Although Bayesian approaches are currently experiencing worldwide growth that is accelerating, historical inertia means that its development remains incipient, especially in peripheral countries.
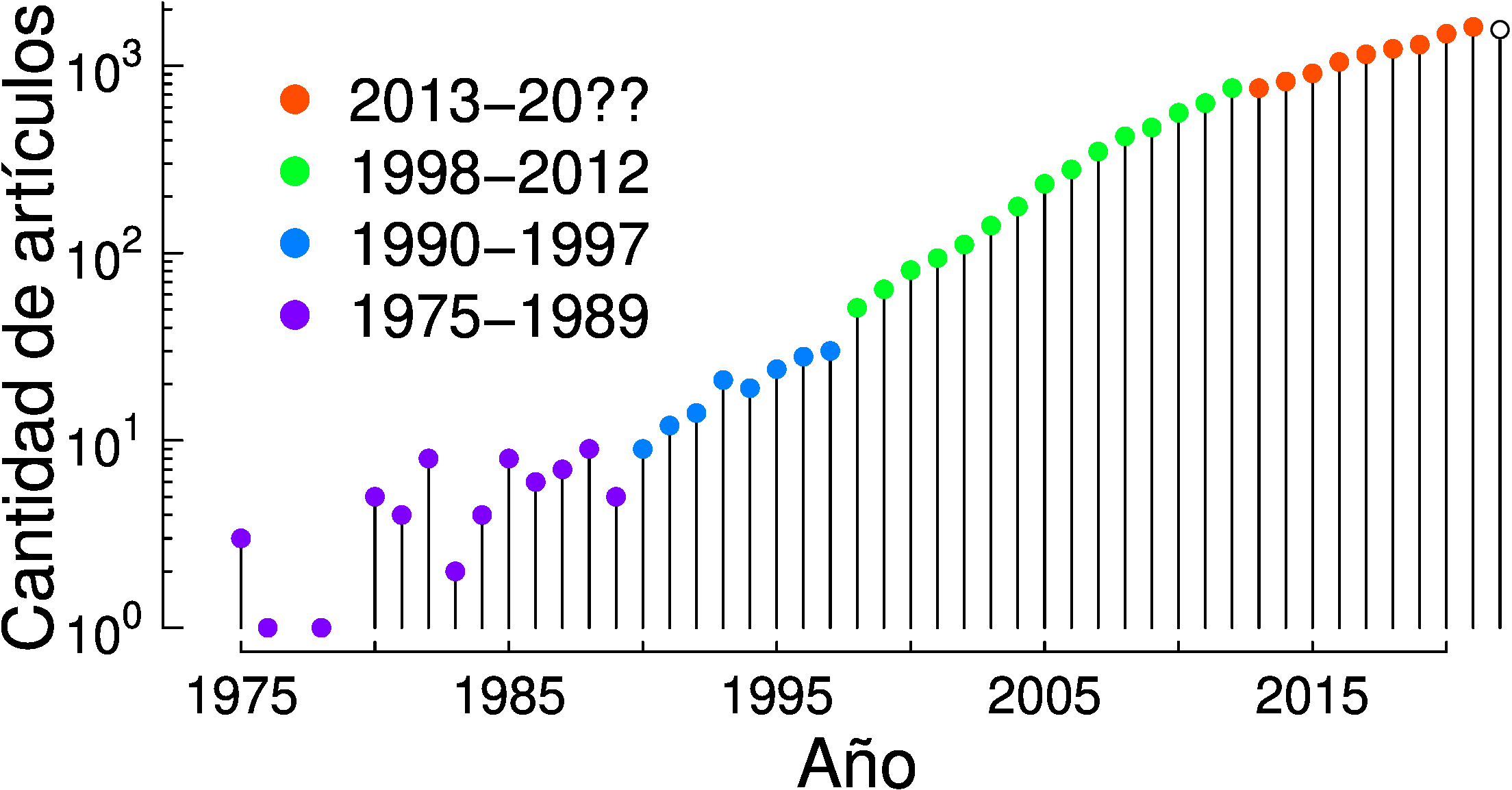
The relevance of these methods contrasts with the current reality in which the Bayesian approach is still marginal even in the most important universities of the Plurinational America, and practically nonexistent in empirical sciences that lack specific training in mathematics and programming. The following figure details the number of scientific articles linked to the Bayesian approach published each year with at least one author affiliation in the Plurinational America according to Scopus.